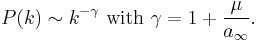Generalized scale-free model

There has been a burst of activity in the modeling of scale-free complex networks. The recipe of Barabási and Albert[1] has been followed by several variations and generalizations[2][3][4][5] and the revamping of previous mathematical works.[6] As long as there is a power law distribution in a model, it is a scale-free network, and a model of that network is a scale-free model.

Contents

Features

Many real networks are scale-free networks, which require scale-free models to describe them. There are two ingredients needed to build up a scale-free model:

1. Adding or removing nodes. Usually we concentrate on growing the network, i.e. adding nodes.

2. Preferential attachment: The probability 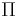\Pi that new nodes will be connected to the "old" node.

Examples

There have been several attempts to generate scale-free network properties. Here are some examples:

The Barabási–Albert model

For example, the first scale-free model, the Barabási–Albert model, has a linear preferential attachment 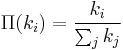\Pi(k_i)=\frac{k_i}{\sum_j k_j} and adds one new node at every time step.

(Note, another general feature of 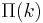\Pi(k) in real networks is that 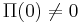\Pi(0)\neq 0, i.e. there is a nonzero probability that a new node attaches to an isolated node. Thus in general 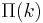\Pi(k) has the form 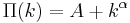\Pi(k)=A %2Bk^\alpha, where A is the initial attractiveness of the node.)

Two-level network model

Dangalchev[7] builds a 2-L model by adding a second-order preferential attachment. The attractiveness of a node in the 2-L model depends not only on the number of nodes linked to it but also on the number of links in each of these nodes.

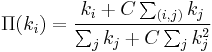\Pi(k_i)=\frac{k_i %2B C \sum_{(i,j)} k_j}{\sum_j k_j %2B C \sum_j k_j^2}, where C is a coefficient between 0 and 1.

Non-linear preferential attachment

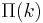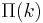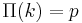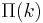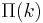The Barabási–Albert model assumes that the probability \Pi(k)that a node attaches to node i is proportional to the degree k of node i. This assumption involves two hypotheses: first, that \Pi(k) depends on k, in contrast to random graphs in which \Pi(k) = p , and second, that the functional form of \Pi(k) is linear in k. The precise form of \Pi(k) is not necessary linear, and recent studies have demonstrated that the degree distribution depends strongly on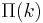 \Pi(k)

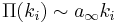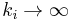Krapivsky, Redner, and Leyvraz[4] demonstrate that the scale-free nature of the network is destroyed for nonlinear preferential attachment. The only case in which the topology of the network is scale free is that in which the preferential attachment is asymptotically linear, i.e. \Pi(k_i) \sim a_\infty k_i as k_i \to \infty. In this case the rate equation leads to

P(k) \sim k^{-\gamma}\text{ with }\gamma = 1 %2B \frac{\mu}{a_\infty}.

This way the exponent of the degree distribution can be tuned to any value between 2 and 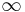\infty.

Hierarchical network model

There is another kind of scale-free model, which grows according to some patterns, such as the hierarchical network model.[8]

The iterative construction leading to a hierarchical network. Starting from a fully connected cluster of five nodes, we create four identical replicas connecting the peripheral nodes of each cluster to the central node of the original cluster. From this, we get a network of 25 nodes (N = 25). Repeating the same process, we can create four more replicas of the original cluster - the four peripheral nodes of each one connect to the central node of the nodes created in the first step. This gives N = 125, and the process can continue indefinitely.

References

  1. ^ Barabási, A.-L. and R. Albert, Science 286, 509 (1999).
  2. ^ R. Albert, and A.L. Barabási, Phys. Rev. Lett. 85, 5234(2000).
  3. ^ S. N. Dorogovtsev, J. F. F. Mendes, and A. N. Samukhim, cond-mat/0011115.
  4. ^ a b P.L. Krapivsky, S. Redner, and F. Leyvraz, Phys. Rev. Lett. 85, 4629 (2000).
  5. ^ B. Tadic, Physica A 293, 273(2001).
  6. ^ S. Bomholdt and H. Ebel, cond-mat/0008465; H.A. Simon, Bimetrika 42, 425(1955).
  7. ^ Dangalchev Ch., Phisica A 338, 659 (2004).
  8. ^ E. Ravasz and Barabási Phys. Rev. E 67, 026112 (2003).